Comprobación de la Ley de Snell con gelatina

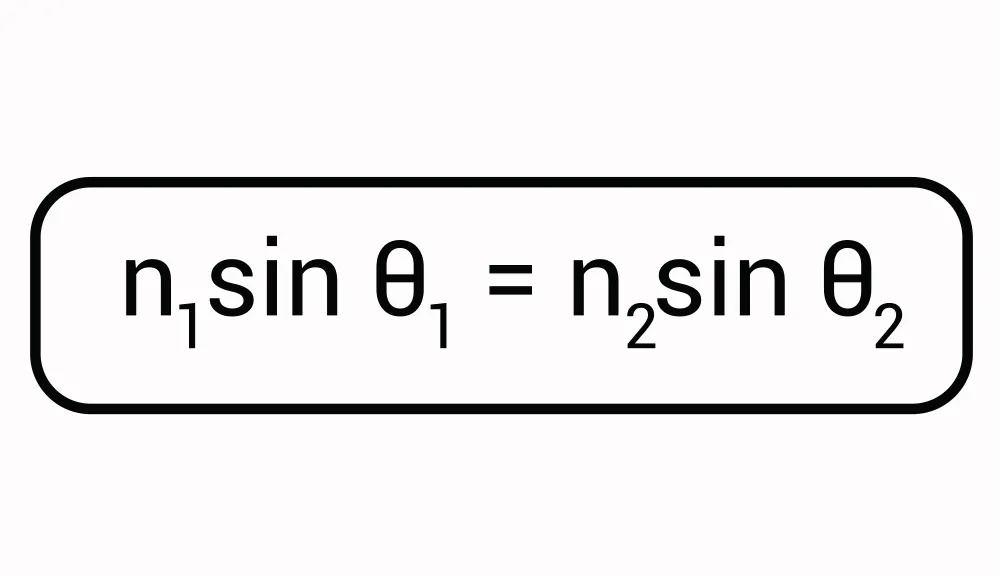
Te compartimos un interesante artículo de la revista +Ciencia de la Facultad de Ingeniería cuyo experimento sobre la Ley de Snell permite un entendimiento mucho más integrado de lo aprendido en clase y ofrece una muestra de la belleza de la ciencia y la ingeniería.

El número 28 de la revista +Ciencia de la Facultad de Ingeniería comparte un artículo en el que el alumno de Ingeniería Biomédica, Diego Vilaboa López, aborda las leyes de Snell, que describen la relación entre el índice de refracción y los cambios angulares de una onda transversal.

Comprobación de la Ley de Snell con gelatina

El trabajo del estudiante no se limita simplemente a absorber información y a sacar buenas calificaciones. Lo hemos escuchado un millón de veces, el objetivo último de este aprendizaje es adquirir la capacidad de aplicar dichos conocimientos en la vida real y en situaciones reales. Sin embargo, ¿qué tan efectivo puede llegar a ser aprenderse una fórmula de memoria si no la entendemos en esencia? Probablemente nos sirva para realizar los exámenes de la materia y a resolver problemas a los que estamos acostumbrados, pero cuando llega la hora de resolver algo más complicado, nos resulta extremadamente difícil ya que las lagunas de conocimiento comienzan a manifestarse y nos petrificamos.
 

Es por esto que el trabajo de laboratorio es tan importante. Este nos permite observar y experimentar de primera mano los fenómenos estudiados durante la clase teórica. Puede que a simple vista no nos demos cuenta de que, durante la práctica, nuestro cerebro está absorbiendo información que trasciende el simple razonamiento lógico que utilizamos para entender el concepto en primer lugar, y conseguimos un entendimiento superior basado en experiencia y razonamiento flexible.

Durante este experimento tuve una experiencia similar a la descrita anteriormente. Yo ya conocía las leyes de Snell, las cuales describen el comportamiento de una onda cuando esta interactúa con diferentes medios, pero mi cerebro no recibió una verdadera asimilación de lo que describe el fenómeno hasta que establecí mis parámetros de medición y los comprobé experimentalmente por mi cuenta.

En resumen, las leyes de Snell describen la relación entre el índice de refracción y los cambios angulares de una onda transversal, como lo es un haz de luz cuando este entra a un medio. La refracción toma lugar justo en la frontera entre dos medios, como lo puede ser el aire y el agua, entonces la luz atraviesa dicha frontera, esta sufre un cambio de dirección, producto de un cambio de velocidad de la onda. 

La luz viaja a una velocidad mayor en el vacío que cuando ésta viaja a través de la atmósfera o en cualquier otro medio en realidad. El grado de este cambio de dirección se denota con base en los ángulos formados por el rayo incidente y el rayo refractado respecto a una línea de referencia. Lo que nos permite la ley de Snell es calcular estos ángulos involucrados a través de la Ecuación 1, donde c es la constante conocida como el índice de refracción entre dos medios y es la proporción de las velocidades de las ondas en sus respectivos medios. El índice de refracción n es una cantidad adimensional pues expresa una mera proporción y tiene como valor default la velocidad de la luz en el aire o en el vacío, cuyo valor sería de 1, excepto en los casos que se especifica otro valor. La fórmula que describe esta relación, la Ecuación 2, se deriva de la fórmula anterior. Mientras más denso sea el medio, mayor será el índice de refracción y menor será la velocidad de la luz en este.

 
Imagen 1. Representación de las leyes de Snell, su relación entre ángulo incidente y rayo refractado

Finalmente, sin entrar mucho en detalle, existe un fenómeno llamado reflexión interna total, que sucede cuando a un cierto ángulo crítico, en el cual la luz que viaja de un medio hacia uno menos denso, no se refracta, por lo que el haz entero de luz queda reflejado internamente en el medio denso sin salir, como si se tratara de un espejo.

Estas son las bases para entender el funcionamiento del experimento. Lo que propuse en mi hipótesis fue que, a partir del fenómeno de reflexión interna total, yo podía medir y modificar el ángulo en el que esta ocurriría siempre y cuando yo variara solamente la concentración de un soluto en una mezcla con el fin de obtener diferentes grados de densidad. Para el experimento, la mezcla sería un cubo de gelatina y el soluto variable sería simplemente la cantidad de grenetina que se utilizó para cada cubo. Mi elección se basó en que necesitaba un medio sólido translúcido cuya densidad yo pudiera controlar sin necesidad de un contenedor que pudiera afectar los fenómenos de luz, por lo que la gelatina era el candidato perfecto. Ahora bien, lo ideal era usar un haz de luz lo más concentrado y visible posible, por lo que la respuesta obvia fue utilizar un dispositivo láser.

La idea se basaba en que mientras más grenetina estuviera disuelta en agua, más denso sería el medio, y, por ende, mayor sería el índice de refracción. Ya que cada índice de refracción tiene diferente efecto sobre la velocidad de la luz, los ángulos deben cambiar. El utilizar el fenómeno de reflexión interna total simplemente fue un parámetro de referencia, pues este fenómeno no depende de factores como la perfección de la orientación del láser o bien su posición, simplemente se toma la captura en el instante en el que ocurre. 

Entonces la variable independiente es la concentración de grenetina con la misma cantidad de agua. La variable dependiente de estas variaciones sería el ángulo crítico, ángulo en el cual sucede la reflexión interna total. Finalmente, las variables controladas son la temperatura de las mezclas, el tiempo que éstas estuvieron en el refrigerador durante su preparación, su forma, además de la frecuencia y potencia del láser. Se realizaron un total de 5 muestras con distintas concentraciones. Estas se muestran en la siguiente tabla junto con la concentración con propagación de errores.

Tabla 1. Determinación de la concentración de gelatina en las muestras realizadas

Al realizar el cociente para obtener la densidad se obtuvo:

Imagen 2. Visualización de la reflexión interna total

En la Imagen 2 vemos al láser en acción antes de que se forme la reflexión interna total. Como se puede apreciar, el láser atraviesa la gelatina y se refracta a través del extremo superior. Vemos la trayectoria del láser a través de la solución, así como el punto donde pega en una hoja a la derecha. Esta imagen es interesante pues se ve claramente el fenómeno de refracción, ya que la trayectoria que traza el láser en la gelatina no concuerda con la dirección que termina adoptando el haz de luz cuando sale del medio.
 

Se compararon gelatinas con diferentes concentraciones, para observar el fenómeno de reflexión interna total y poder medir sus ángulos críticos mediante un software. El ángulo obtenido de la gelatina de menor concentración fue de 48.31°, mientras que la de mayor concentración fue de 41.41°.

Entonces, fue posible determinar que la mezcla con mayor concentración tiene reflexión interna total a un menor ángulo que la de menor concentración. Esto tiene sentido, ya que la fórmula que describe al ángulo crítico y al índice de refracción es 1/Sin0 crítico=n la cual indica que, a menores valores del ángulo crítico, mayores índices de refracción obtenemos, y, como hemos visto anteriormente, altos índices de refracción denotan altas densidades del medio. 

Una forma de razonarlo es que mientras más denso es el medio, mayor es el cambio de velocidad de la onda cuando ésta sale de éste, por lo que el cambio de dirección es más pronunciado. Por esto mismo, no se necesitan grandes cambios en la inclinación del láser para que la luz se desvíe lo suficiente para provocar la reflexión interna total. Se podría decir que el fenómeno se manifiesta “antes” si vamos aumentando el ángulo empezando desde 0 grados respecto a la horizontal cuando el medio es más denso. En la siguiente tabla se presentan los datos de cada una de las muestras ya con el índice de refracción calculado para cada medio/mezcla.

Tabla 2. Ángulos críticos e índices de refracción

Los resultados del experimento no solo apoyan que es posible determinar concentraciones de solutos en sustancias con los fenómenos de refracción, sino que, como se dijo anteriormente, permite un entendimiento mucho más integrado de lo aprendido en clase y nos da una pequeña probada de la belleza de la ciencia y la ingeniería cuando estas se aplican en el mundo real. 
*Colaboración del alumno Diego Vilaboa López (2º semestre de Ingeniería Biomédica).

Da clic en la portada para conocer la revista completa

Para más artículos interesantes como este, te invitamos a consultar +Ciencia, la revista cuatrimestral de la Facultad de Ingeniería, que en cada número tiene contenido relevante de sus alumnos e investigadores. Da clic aquí para conocer todas las ediciones.